>This is a short program that uses Java's built in Random number generator to generate random numbers from a discreet arbitrary distribution. I am applying this program to seed a stochastic simulation with a distribution obtained from a steady state PDE model.
The input is a double array, where each double is the relative magnitude that the index should occur. Essentially it is a probability distribution, but it does not have to be normalized.
import java.util.Random;
/**
*For picking random numbers from an arbitrary distribution.
*
* Date: 7/29/11
* Time: 3:57 PM
*/
public class DistributionPicker {
Random number_generator;
double[] normalized_rates;
/**
* Constructs with a default Random object. Still
* needs to be initilized with a distribution.
*
*/
public DistributionPicker(){
number_generator = new Random();
}
public DistributionPicker(Random ng){
number_generator = ng;
}
/**
*
* Creates a normalized distribution from a data set for picking values.
* @param d - the data sets with relative values, this set will be normalized.
* Negative cause an exception to be thrown.
*
*/
public void setData(double[] d){
normalized_rates = new double[ d.length];
double sum = 0;
for(double value: d){
if (value<0) throw new IllegalArgumentException("Distributions cannot be negative");
sum+= value;
}
for(int i = 0; i<d.length; i++){
normalized_rates[i] = d[i]/sum;
}
}
/**
* returns the fractional value of the next number, where the integer portion
* represents the index of the values and the double is the 'depth'
* into that index.
*
*/
public double nextDouble(){
double sum = 0;
double fraction = number_generator.nextDouble();
int i;
double v=1;
for(i = 0; i<normalized_rates.length; i++){
v = normalized_rates[i];
if (sum + v >= fraction){
break;
}
sum += v;
}
double left = (fraction - sum)/v;
return i + left;
}
/**
* For verifying distribution values.
*
* @param args
*/
public static void main(String[] args){
testDistribution(new double[]{1,2,0,0.1});
double[] exponential = new double[100];
System.out.println("##");
System.out.println("##");
for(int i = 0; i<100; i++){
exponential[i] = Math.exp(-(i/20.0));
}
testDistribution(exponential);
}
/**
* Prints out a list of numbers for the supplied distribution.
*
* @param distribution
*/
public static void testDistribution(double[] distribution){
double[] pick_histogram = new double[distribution.length*10];
DistributionPicker picks = new DistributionPicker();
picks.setData(distribution);
double n = 100000;
double delta = 10/n;
for(int i = 0; i<100000; i++){
double next = picks.nextDouble();
int dex = (int)(10*next);
pick_histogram[dex] += delta;
}
for(int i = 0; i<pick_histogram.length; i++){
System.out.println(
i + "\t" +
pick_histogram[i] + "\t" +
(picks.normalized_rates[(int)(i/10.0)])
);
}
}
}
The main method performs two checks to verify that the distributions are correct. The first distribution is to show how the bins are setup. The first bin has a relative probability of 1, which means that about 30% of the time a number between 0 and 1 will be picked. The resulting distributions look like this.
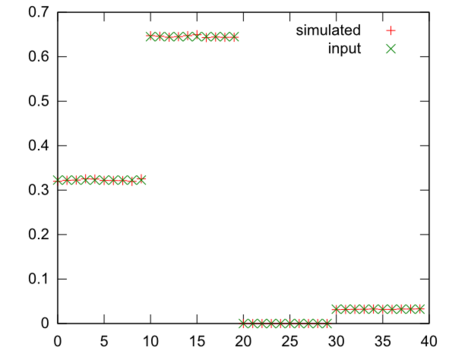
(note I used more points that shown above so the curves are very close).
The next distribution is an exponential distribution.
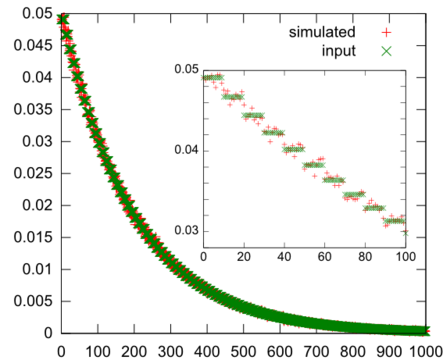
Since we are only approximating an exponential you can see the steps in the insert. Also since there are more bins the result is a bit noisy.
Why does this work? We are using an equivalent distribution,
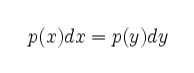
Where we pick some number x from a known distribution (uniform distribution) and we want to know the corresponding value of y. This is achieved by integrating the distributions. To integrate the y distribution we assume each bin has a uniform probability. The integration of y is performed each time the nextDouble method is called. The integral of the x distribution for any x is x.