>The Gillespie algorithmWikiPedia Of Algorithm finds the time it takes for this 1-d Model to step one space forward. I am comparing this to a model where after discrete a discrete timestep it is randomly determined whether or not the item 'stepped'
At a rate of 0.01 we can see good correlation between the two algorythms.
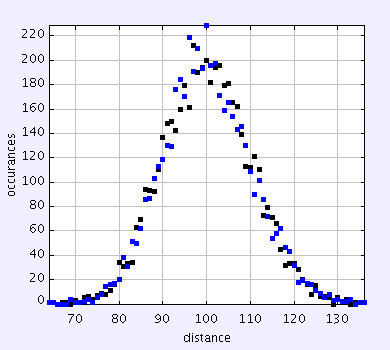
As the rate increases to 0.1 the is a hint of a difference but not to distinct.
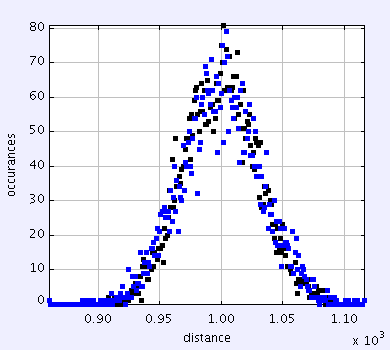
The standard deviations become to be noticeably different. 893 for the descrete method and 1040 for the Gillespie method.
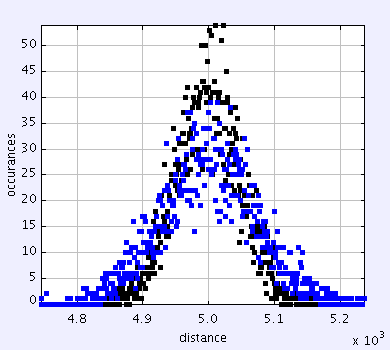
Now the differences are much larger and the standard deviation is noticeably different. 2430 versus 5970. Lastly we look at a rate of 0.9 times per second.
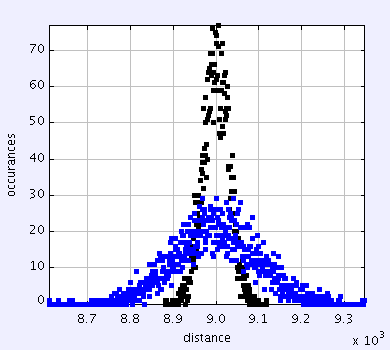
And the standard deviation is about 900 versus 9000. One of the important features here is the Gillespie algorithm leads to an increase in standard deviation while the discrete method actually leads to a decrease.
Clearly we must consider the fact that the values are being taken discretely so I will change my sampling rate from 1 per second to what ever rate gives me a probability of 0.01.
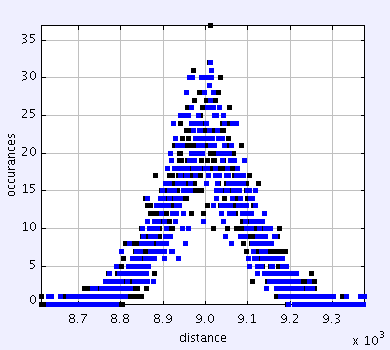
and this example produced a std deviation of 8970 vs 9180 which is about 20% which still isn't great. It also came at a huge computing dissadvantage. Where as previoulsy the computation ran in under 20 seconds for both this took around 5 minutes to complete.